Augmented Reality
Objective

Brief Description of the approach followed
-
Camera Calibration
First, we recorded a video of a 9x7 chessboard using a laptop’s webcam. Using multiple frames of this video, we found out 8x6 chess board in each frame and its corners with the help of OpenCV library. Then we refined the corners to subpixels & finally found the intrinsic camera matrix, and distance coefficients using OpenCV library functions.

-
Visual Markers
We experimented with multiple visual markers to use as planar template objects.
- 6x6 ArUco markers

- Simple playing cards

- 6x6 ArUco markers
-
Marker Detection
- Based on the template images, the task was to now detect the markers in a video which was pre-recorded.
- This was done by first finding feature descriptors like SIFT, ORB, SURF etc. and then finding matches between each frame and template image.
- Then homography is estimated using matching points which were refined using
RANSACandLowe’s test.
-
Rendering Object On Marker
- After finding the homography, we find the projection matrix.
- We then use this projection matrix to render an object (read from a
.objfile) on to the frame of the video.

-
Moving a Marker Until Hitting Another
- Now, the first time we observe a marker of ArUco id=1. We place the object there, saving the projection matrix and start translating the object in one direction parallel to the plane.
- This is achieved by finding \(P' = P \times M\) where \(P'\) and \(P\) are the new & old projection matrix respectively. \(M\) corresponds to the movement matrix where \(M = [I \mid T]\) and \(T = [0, x, 0]^{T}\). Here, \(x\) is incremented in each frame based upon a rate.
- In order to stop the car, we observe that the car’s front corner pixel, \(p\) in the other frame’s coordinates. We have the car’s extrinsic matrix \(S\), the wall’s extrinsic matrix \(E\). Since, \(S = E \times X \rightarrow X = E^{-1}S\). Then, \(p\)’s coordinate in wall’s frame of reference can be given by \(p_{W} = X \times p\).
- Thus, we check \((X \times p)\)’ s \(z\)-coordinate to see when it would hit the plane. When it does so, we stop the car from translating further.


-
Projecting multiple objects on the same scene
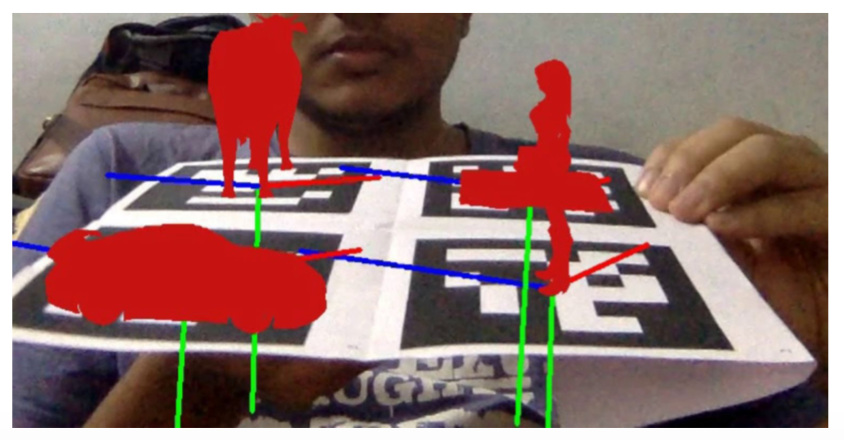
Other results have been mentioned in this link along with a comprehensive report.

